Data Representation in Computer

Data refers to the symbols that represent people, events, things, and ideas. Data can be a name, a number, the colors in a photograph, or the notes in a musical composition

Data Representation refers to the form in which data is stored, processed, and transmitted. Devices such as smartphones, iPods, and computers store data in digital formats that can be handled by electronic circuitry.

Digitization is the process of converting information, such as text, numbers, photos, or music, into digital data that can be manipulated by electronic devices.

The Digital Revolution has evolved through four phases, beginning with big, expensive, standalone computers, and progressing to today’s digital world in which small, inexpensive digital devices are everywhere.

Introduction

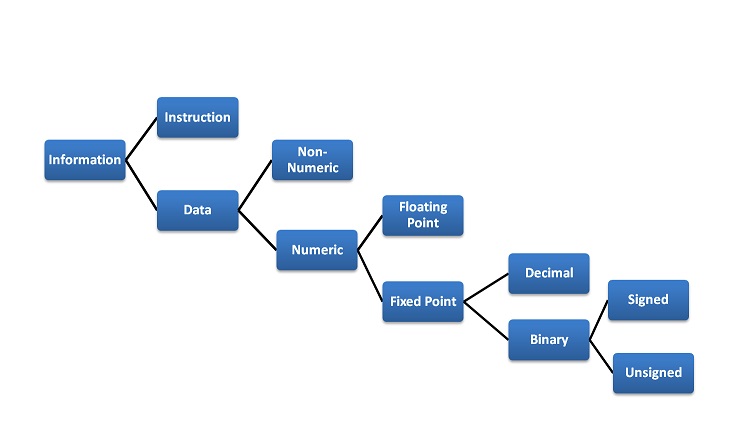
Data stored in different kinds

1. Numeric (0, 1, 2..9)
2. Alphabetic (A, B, C…Z)
3. Alphanumeric
4. Special Characters

All of them are represented in terms of 0s and 1sAnd their unique combinations

Our discussion is focused on the following number systems:

1. Decimal number
2. Binary number system,
3. Octal number system, and
4. Hexadecimal number system

Base or Radix

Base / Radix	Name
2	Binary system
8	Octal system
10	Decimal system
16	Hexadecimal system

NUMBER SYSTEM

Face value

The face value of a digit in a number is the value of the digit itself. Wherever it appears.

Place value/Position Value

The place value of a digit in a number is the value of the digit where it appears.

E.g.

1. 768534, find place value and face value of 5 in given no;

Face Value of 5 is; 5

Place Value of 5 is; 5*100= 500

2. 0.03721; find place value of 3.

Another way;

The Place Value/Position value of a digit is 【Base^Position】

In 768534 Place Value/Position value 5 is = 10²–>5*10²

A number in a particular base is written as 【(number)_{base of number}】For example, (23)₁₀ means that the number 23 is decimal (345)₈ shows that 345 is an octal number.

1. Decimal Number System

It consists of 10-digit numbers—0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

probably the most commonly used number system

All numbers in this numbering system are a combination of 0-9 digits

Represented by base or radix 10/ base 10 number system

Position	3	2	1	0	-1	-2	-3
Position Value	103	102	101	100	10-1	10-2	10-3
Quantity	1000	100	10	1	1/10	1/100	1/1000

1. Binary Number System

The binary number system consists of two digits—0 and 1.

All binary numbers are formed using a combination of 0 and 1.

All numbers in this numbering system are unique combinations of 1’s & 0’s

Represented by base or radix 2

Position	3	2	1	0	-1	-2	-3
Position Value	23	22	21	20	2-1	2-2	2-3
Quantity	8	4	2	1	1/2	1/4	1/8

1. Octal Number System

The octal number system consists of eight digits—0 to 7.

All octal numbers are represented using these eight-digit

Also called“oct” in short, is the base-8 number system

Position	3	2	1	0	-1	-2	-3
Position Value	83	82	81	80	8-1	8-2	8-3
Quantity	512	64	8	1	1/8	1/64	1/512

1. HexaDecimal Number System

The hexadecimal number system consists of sixteen digits—0 to 9, A, B, C, D, E, F, where (A is for 10, B is for 11, C-12, D-13, E-14, F-15).

All hexadecimal numbers are represented using these 16 digits.

In short “hex”

Base 16 Number System

Position	3	2	1	0	-1	-2	-3
Position Value	163	162	161	160	16-1	16-2	16-3
Quantity	4096	256	16	1	1/16	1/256	1/4096

 

Decimal	Binary	Octal	Hexadecimal
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

 

Signed and Unsigned Numbers:

Signed Numbers:

-Definition: Signed numbers are integers that can be either positive or negative. They include a sign (plus or minus) to indicate the value’s polarity.

Representation: Typically, in binary systems, signed numbers are represented using two’s complement, sign-and-magnitude, or one’s complement methods.

  Two’s Complement: The most common method. The most significant bit (MSB) is the sign bit (0 for positive, 1 for negative). It simplifies arithmetic operations and negation.

  Sign-and-Magnitude: The MSB represents the sign, and the remaining bits represent the magnitude. Less common due to more complex arithmetic operations.

  One’s Complement: The negative number is represented by inverting all bits of the positive number.

Range: For an n-bit signed number using two’s complement, the range is from -2^(n-1) to 2^(n-1) – 1. For example, an 8-bit signed number ranges from -128 to 127.

Applications: Used in scenarios where both positive and negative values are required, such as temperature measurements, financial calculations, and balance sheets.

 

Unsigned Numbers:

Definition: Unsigned numbers are non-negative integers. They do not include a sign bit, meaning all bits are used to represent the magnitude of the number.

Representation: In binary, all bits contribute to the magnitude, with no consideration for positive or negative values.

Range: For an n-bit unsigned number, the range is from 0 to 2^n – 1. For example, an 8-bit unsigned number ranges from 0 to 255.

Applications: Used in scenarios where only non-negative values make sense, such as counting objects, indexing arrays, and measuring lengths.

 

 Key Differences:

Sign Representation: Signed numbers include a sign bit, whereas unsigned numbers do not.

Range: Signed numbers have a range that includes negative values, reducing the positive range. Unsigned numbers have a larger positive range since they exclude negative values.

Use Cases: Signed numbers are essential for calculations requiring negative values, while unsigned numbers are suitable for counting and indexing where negative values are meaningless.

 

Understanding these concepts is crucial in computer science and programming, as they affect how data is stored, processed, and interpreted in various applications.