A Boolean functions are an algebraic expression made up of binary variables (e.g., 0s and 1s), logical operations (AND, OR, NOT), and constants. In digital logic design, Boolean functions represent logic circuits, determining how inputs map to outputs. The primary goal of simplifying Boolean functions is to create efficient, cost-effective, and power-saving circuits.
Table of Contents
ToggleWhy Simplify Boolean Functions?
- Minimizes Hardware Cost: Simplified circuits use fewer gates and connections.
- Increases Circuit Speed: Fewer gates generally reduce the propagation delay.
- Reduces Power Consumption: Using fewer gates means less power consumption.
- Improves Reliability: With fewer components, there’s less chance of failure.
- Facilitates Easier Testing and Maintenance: Simplified circuits are easier to analyze and troubleshoot.
Methods of Simplifying Boolean Functions
There are multiple approaches for simplifying Boolean functions, each suited for different levels of complexity. Here, we’ll cover the main methods:
Algebraic Simplification
This method involves using Boolean algebra rules to rewrite expressions in a simpler form. Some key rules include:
- Identity Laws: A+0=A and A⋅1=A
- Null Laws: A+1=1 and A⋅0=0
- Idempotent Laws: A+A=A and A⋅A=A
- Complement Laws: A+A‾=A and A⋅A‾=0
- Distributive Law: A+(B⋅C)=(A+B)⋅(A+C)
Example:
Suppose we have the expression:
F=A⋅(B+C)+A⋅B
Using distributive law and simplification:
F=A⋅B+A⋅C+A⋅B=A⋅(B+B)+A⋅C=A⋅1+A⋅C=A
Karnaugh Maps (K-Maps)
K-Maps provide a graphical way to simplify Boolean functions, especially effective for up to six variables. The map is a grid that represents all possible input combinations, where adjacent cells differ by only one bit. Here’s how the process works:
- Plot the Truth Table: Determine the output values for all combinations of inputs.
- Create Groups of 1’s: Look for clusters of 1’s in powers of two (e.g., groups of 2, 4, or 8).
- Identify Prime Implicants: Each group represents a simplified product term.
- Write the Simplified Expression: Use the largest groups possible to minimize terms.
Example:
For a function with three variables, say F(A,B,C)F(A, B, C)F(A,B,C), with output 1’s in cells corresponding to minterms 1,3,5,71, 3, 5, 71,3,5,7:
- Place these 1’s on the K-Map.
- Group adjacent 1’s (e.g., forming a 4-cell group if possible).
- Derive a minimized expression based on the groupings.
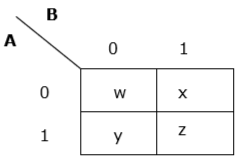
Example 1
An arbitrary truth table is taken below −
| A | B | A operation B |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
Now we will make a k-map for the above truth table −
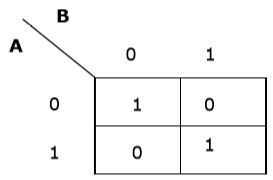
Example 2
Now we will make a K-map for the expression − AB+ A’B’
Simplification Using K-map
K-map uses some rules for the simplification of Boolean expressions by combining together adjacent cells into single term. The rules are described below −
Rule 1 − Any cell containing a zero cannot be grouped.
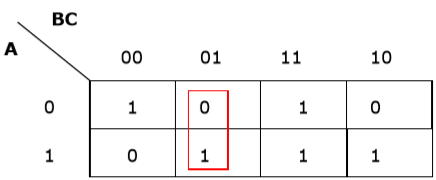
Wrong grouping
Rule 2 − Groups must contain 2n cells (n starting from 1).
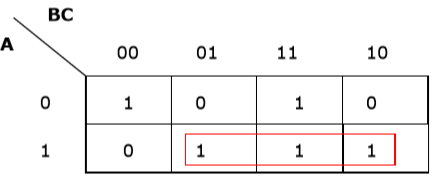
Wrong grouping
Rule 3 − Grouping must be horizontal or vertical, but must not be diagonal.
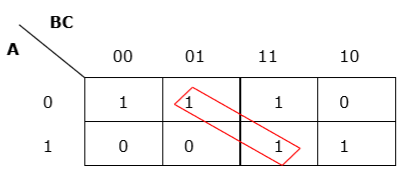
Wrong diagonal grouping
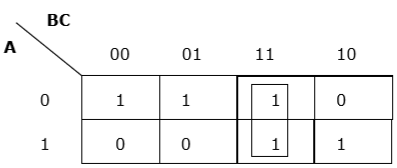
Proper vertical grouping
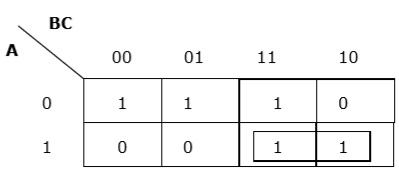
Proper horizontal grouping
Rule 4 − Groups must be covered as largely as possible.
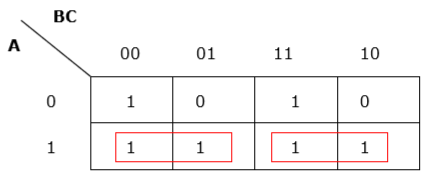
Insufficient grouping
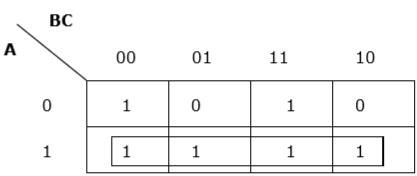
Proper grouping
Rule 5 − If 1 of any cell cannot be grouped with any other cell, it will act as a group itself.
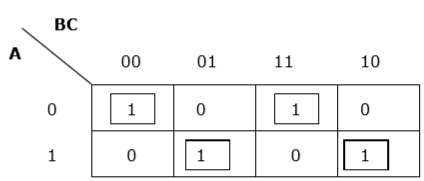
Proper grouping
Rule 6 − Groups may overlap but there should be as few groups as possible.
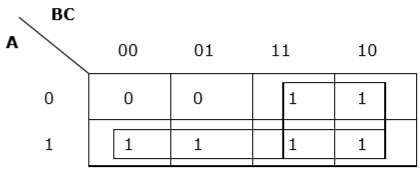
Proper grouping
Rule 7 − The leftmost cell/cells can be grouped with the rightmost cell/cells and the topmost cell/cells can be grouped with the bottommost cell/cells.
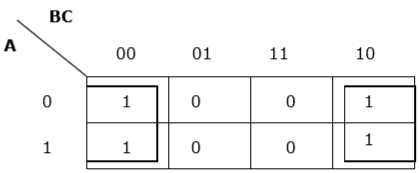
Proper grouping
Quine-McCluskey Method
The Quine-McCluskey method is a systematic approach for simplifying Boolean functions, particularly useful for functions with more than four variables. It’s a two-step process:
- Prime Implicant Generation:
- List all minterms in terms of binary representations.
- Group minterms with the same number of 1’s and combine adjacent terms that differ by only one bit.
- Prime Implicant Chart:
- List all essential prime implicants that cover all minterms.
- Choose a minimal set of prime implicants that covers the function.
This method ensures minimal expressions but can be computationally intensive for large functions.
Espresso Method
The Espresso algorithm is a computational approach used in software design tools to handle complex functions with a large number of variables. It uses heuristics to reduce redundant terms and simplify expressions quickly, making it ideal for large-scale digital systems like those in microprocessor and communication designs.
Comparison of Simplification Methods
| Method | Best For | Pros | Cons |
|---|---|---|---|
| Algebraic | Simple expressions | Easy to understand | Ineffective for large expressions |
| Karnaugh Maps | Up to 6 variables | Visual and intuitive | Difficult with more than 4-6 variables |
| Quine-McCluskey | More than 4 variables | Guarantees minimum solution | Computationally heavy |
| Espresso | Large and complex functions | Fast and efficient | May not give absolute minimal solution |
Applications of Boolean Simplification in Digital Logic
Simplification of Boolean functions is critical across various applications in digital logic:
- Digital Circuits: Simplified Boolean functions translate to simpler circuits, reducing the number of gates and the complexity of ICs (Integrated Circuits).
- Embedded Systems: Embedded systems benefit from simpler circuits, which minimize power usage and improve response time in resource-constrained environments like IoT and automotive systems.
- Data Transmission: In digital communication, encoding and decoding circuits require minimized Boolean functions for fast and efficient data processing.
- Control Systems: In industrial automation and robotics, PLCs (Programmable Logic Controllers) rely on Boolean simplification for real-time responses and efficient control of machinery.
Examples of Simplification of Boolean Funcions
Let’s simplify a Boolean function step-by-step using different methods.
Example 1: Algebraic Simplification
Given: F=AB+AB+A
1 Apply the Absorption Law: A+AB=A
F=A+AB=A
Example 2: Karnaugh Map Simplification
Consider:
F(A,B,C)=∑(1,3,5,7)
Using a K-Map:
- Plot the minterms and form groups.
- Simplified expression might become A⋅C, for instance.
Example 3: Quine-McCluskey Simplification
Suppose:
F(A,B,C,D)=∑(1,3,7,11,15)
- List minterms in binary and group by 1-count.
- Combine terms and create prime implicants.
- Cover all minterms with the smallest set of implicants.
Simplifying Boolean functions is essential for creating efficient digital circuits. By reducing the number of terms in Boolean expressions, engineers minimize hardware, improve speed, and reduce power usage in circuits. Depending on the complexity, designers can use algebraic methods, Karnaugh Maps, Quine-McCluskey, or computational methods like Espresso to achieve optimal results.