A combinational circuit, also called a combinational logic circuit, is a digital electronic circuit whose output is determined only by present inputs. In other words, a combinational circuit is a digital logic circuit whose output depends only on the present input values and does not depend on any feedback or previous input or output values.
Table of Contents
ToggleIntroduction to Combinational Logic
Combinational logic is a type of digital logic where the output at any time depends only on the current values of the inputs, not on any past inputs. Unlike sequential logic, which involves memory elements and stores past states, combinational logic operates without any memory of previous states.
Common applications of combinational logic include arithmetic circuits, multiplexers, encoders, decoders, and comparators. Understanding combinational circuits is essential because they form the foundation of more complex digital systems.
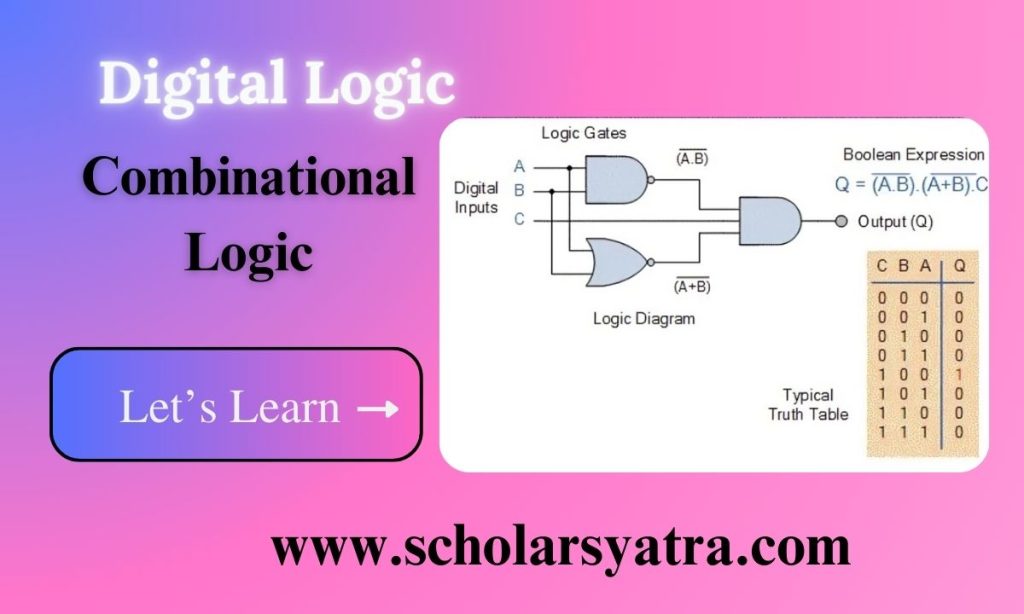
Block Diagram of Combinational Circuit
The following figure depicts the block diagram of a combinational logic circuit.
Here, we can see that there are only three key elements in the circuit diagram of a combinational circuit, they are:
- Input Lines: The input lines are used to enter the input values into the combinational circuit.
- Processing Unit: It is the main element that processes the input values depending on the type of the circuit. For example, a full adder adds three binary bits.
- Output Lines: The output lines are used to take results generated by the circuit.
Basic Components of Combinational Logic
The building blocks of combinational logic circuits are logic gates. These gates process binary inputs (0s and 1s) and produce outputs based on Boolean functions. The primary logic gates are:
- AND Gate: Outputs 1 only if all inputs are 1.
- OR Gate: Outputs 1 if at least one input is 1.
- NOT Gate (Inverter): Outputs the opposite of the input (0 becomes 1, and 1 becomes 0).
Other commonly used gates include:
- NAND Gate: Outputs 0 only if all inputs are 1. (AND followed by NOT)
- NOR Gate: Outputs 1 only if all inputs are 0. (OR followed by NOT)
- XOR Gate: Outputs 1 if the number of 1s in the inputs is odd.
- XNOR Gate: Outputs 1 if the number of 1s in the inputs is even.
These gates are represented by specific symbols in circuit diagrams and can be combined to form more complex logic functions.
Boolean Algebra and Truth Tables
Boolean algebra is the mathematical system used to describe combinational logic. It uses variables (usually denoted by letters such as A, B, C) that represent binary values. Boolean expressions are combinations of variables and operators (AND, OR, NOT) and are used to specify the behavior of a combinational circuit.
Truth Tables
A truth table is a table that lists all possible input combinations for a logic function and the corresponding output. Truth tables provide a clear way to visualize how a logic function behaves with different inputs.
For example, here’s the truth table for a 2-input AND gate:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The output of an AND gate is only 1 when both A and B are 1.
How to make a Combinational Circuit?
The design of combinational circuits involves creating Boolean expressions and then implementing them using logic gates. The main steps are:
- Define the Problem: Specify what the circuit needs to accomplish, usually as a set of output requirements based on input conditions.
- Formulate the Truth Table: Create a truth table that lists all possible input combinations and desired outputs.
- Write the Boolean Expression: Using the truth table, write the Boolean expression(s) for each output. You can use minterms (ANDed terms that represent each row where the output is 1) or maxterms (ORed terms that represent each row where the output is 0).
- Simplify the Expression: Simplify the Boolean expression using Boolean algebra rules or Karnaugh maps (K-maps), which help minimize the number of gates in the circuit.
- Draw the Logic Diagram: Finally, draw the circuit diagram using logic gates according to the simplified Boolean expression.
Example: Half-Adder Circuit
A half-adder is a combinational circuit that adds two binary digits and outputs a sum and carry.
- Define the Problem:
- Inputs: A and B (two single-bit binary values)
- Outputs: Sum (S) and Carry (C)
- Truth Table:
A B S (Sum) C (Carry) 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 - Boolean Expressions:
- Sum (S) = A XOR B
- Carry (C) = A AND B
- Logic Diagram:
- Connect an XOR gate for Sum and an AND gate for Carry.
5. Types of Combinational Circuits
In digital electronics, the combinational circuits are important components of digital systems. Depending on the functions performed, there are various types of combinational circuits. Some common types of combinational circuits and their functions are explained below:
- Adders
- Half-Adder: Adds two binary digits, producing a Sum and Carry.
- Full-Adder: Adds three binary digits (including a carry-in from a previous stage), producing a Sum and Carry.
- Multiplexers (MUX)
- A multiplexer selects one of several input signals and outputs that selected input. A multiplexer has select lines that determine which input is sent to the output.
- Decoders
- A decoder takes an n-bit binary input and activates one of its 2^n outputs. Used in applications where one signal must be selected out of many options.
- Encoders
- An encoder does the reverse of a decoder: it converts 2^n inputs into an n-bit output.
- Comparators
- Comparators compare two binary numbers and output a signal based on whether one is greater than, less than, or equal to the other.
Simplifying Combinational Logic: Karnaugh Maps (K-maps)
A Karnaugh map (K-map) is a visual tool for simplifying Boolean expressions, especially helpful for circuits with 3 to 6 variables. By arranging truth table values in a K-map, you can easily identify patterns of adjacent 1s or 0s, allowing you to create simplified Boolean expressions.
Steps to Use a K-map
- Set Up the K-map: Each cell represents a unique combination of input variables.
- Populate the K-map: Fill in the cells with values from the truth table.
- Group Adjacent Cells with 1s: Look for groups of 1s (powers of 2: 1, 2, 4, 8, etc.) that can be combined to form simplified terms.
- Write the Simplified Expression: Use the grouped cells to write a minimized Boolean expression.
Practical Example of Simplifying a Circuit Using a K-map
Suppose we have a truth table with three inputs, A, B, and C, and one output, F, based on a certain logic function.
| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Place the outputs in the K-map, group them, and derive a simplified Boolean expression.
Limitations of Combinational Logic
Combinational circuits have several advantages such as fast operational speed, simpler circuits, predictable operation, etc. However, they do have several limitations too, some of which are listed below:
- No Memory: Combinational circuits lack memory, meaning they cannot store any previous states or information. The output solely depends on the current input, making them ineffective for applications requiring historical data or previous states.
- Larger Circuits Become Complex: As the number of inputs increases, combinational circuits can become large, complex, and challenging to simplify. Managing and designing circuits with many inputs requires extensive logic gates, which can increase cost and power consumption.
- Glitches and Propagation Delay: Combinational circuits are subject to propagation delay (the time it takes for the output to respond to an input change). This delay can result in temporary incorrect outputs, called “glitches,” particularly in larger circuits. While techniques can mitigate glitches, the delay can still impact performance in high-speed applications.
- Limited to Specific Functions: Combinational circuits are best suited for tasks where each output depends on a combination of current inputs. They are not suitable for tasks that need feedback or iterative processing, such as state-based control systems.
- Limited Scalability for Complex Logic: Scaling combinational logic circuits to handle highly complex functions can be impractical, as the number of logic gates and wiring can grow exponentially with additional inputs and outputs. This leads to design challenges, higher power consumption, and increased difficulty in troubleshooting.
Applications of Combinational Logic
Despite their limitations, combinational logic circuits are widely used in a range of digital systems due to their speed and efficiency for certain types of tasks. Here are some common applications:
- Arithmetic and Logic Units (ALUs): Combinational logic forms the core of arithmetic and logic units in CPUs, where binary addition, subtraction, and logical operations (like AND, OR, NOT) are executed. Circuits like adders, subtractors, and multiplexers are essential components in ALUs.
- Data Selection and Routing:
- Multiplexers (MUX): MUX circuits select one of many input data lines and route it to a single output, based on control signals. This is crucial in data routing applications and digital communications.
- Demultiplexers (DEMUX): DEMUX circuits route a single input to one of several output lines, commonly used in digital broadcasting and network data distribution.
- Encoding and Decoding:
- Encoders: Convert a set of inputs into a coded binary output, useful in applications where data needs to be compacted or labeled.
- Decoders: Convert coded binary data into distinct output lines, such as in seven-segment displays and memory address decoding.
- Binary Comparators: Combinational logic comparators are used in digital systems to compare binary values. These comparators are applied in sorting algorithms, decision-making circuits, and digital controllers to determine if a value meets certain criteria.
- Digital Signal Processing (DSP): Combinational logic is used in various DSP applications, such as in filters, encoders, and decoders, where high-speed, non-sequential processing is required.
- Code Conversion: Certain applications require converting data between binary codes, such as Binary Coded Decimal (BCD) to 7-segment code for digital displays. Combinational circuits simplify these conversions.
- Error Detection and Correction: Combinational logic can implement error detection codes, such as parity generators and checkers, which are widely used in data storage and transmission systems to ensure data integrity.
- Basic Control Systems: Simple control systems where output actions are solely based on current inputs (e.g., light switches, combinational locks, digital circuits for relay controls) often employ combinational logic circuits.