Concept of Number System

Conversion of Number System

Binary to Decimal Conversion:

• To convert a binary number to a decimal, multiply each bit by 2n2^n2n, where n is the position of the bit from right to left, starting at 0.

Example:

• Convert 1101 to decimal:

  1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 8 + 4 + 0 + 1 = 13

   

Decimal to Binary Conversion:

• To convert a decimal number to binary, repeatedly divide the number by 2, noting the remainder at each step, until the quotient is 0. The binary number is read from bottom to top (least significant bit to most significant bit).

Example:

• Convert 25 to binary:

25 ÷ 2 = 12, remainder 1
12 ÷ 2 = 6, remainder 0
6 ÷ 2 = 3, remainder 0
3 ÷ 2 = 1, remainder 1
1 ÷ 2 = 0, remainder 1
Binary representation: 11001

Hexadecimal and Octal Conversions:

• Hexadecimal (base-16) and octal (base-8) are other numeral systems often used in computing. They can be converted to and from binary more easily than decimal.
• Hexadecimal to Binary: Each hex digit converts to a 4-bit binary equivalent.
• Octal to Binary: Each octal digit converts to a 3-bit binary equivalent.

Examples:

• Hex 1A3 to binary: 0001 1010 0011
• Octal 47 to binary: 100 111

Logic Gates and Binary Logic

• AND Gate: Outputs 1 only if both inputs are 1.
  • Truth Table:
    

    A	B	Output
    0	0	0
    0	1	0
    1	0	0
    1	1	1

• OR Gate: Outputs 1 if at least one input is 1.
• NOT Gate: Outputs the inverse of the input (1 becomes 0, and 0 becomes 1).
• NAND, NOR, XOR, and XNOR Gates: Variations that perform specific logical operations useful in digital circuits.

Applications of Binary Number System

• Data Storage: All digital data, from simple text to complex multimedia, is stored in binary format.
• Machine Code and Assembly Language: Machine-level instructions use binary representations for operations and data.
• Digital Circuit Design: Understanding binary logic is crucial for designing flip-flops, multiplexers, and other components in digital electronics.

Complements in Number System

Complements are mathematical methods used for simplifying the subtraction of numbers by converting it into an addition problem. In digital logic, they are used for representing negative numbers and performing binary arithmetic operations efficiently. There are two general types of complements: r’s complement and (r-1)’s complement, applicable to different base systems.

1. (r-1)’s Complement

The $(r-1)$‘s complement of a number is obtained by replacing each digit of the number with the highest digit in the base minus the digit itself. This concept is applicable to any base system, with the most common being binary ($r=2$) and decimal ($r=10$).

Explanation for Different Base System

• Decimal (Base 10):
  • (10-1)’s complement (9’s complement): To find the 9’s complement of a decimal number, replace each digit with $9-\text{digit}$.
  • Example:
    • Find the 9’s complement of 4567:
      • Replace each digit: $9-4=5$, $9-5=4$, $9-6=3$, $9-7=2$.
      • Result: 5432.
• Binary (Base 2):
  • (2-1)’s complement (1’s complement): To find the 1’s complement of a binary number, replace each 0 with 1 and each 1 with 0.
  • Example:
    • Find the 1’s complement of 1010:
      • Result: 0101.

Properties of (r-1)’s Complement:

• Used for subtraction by adding the $(r-1)$‘s complement of the subtrahend to the minuend and handling any carry if needed (especially in the case of 1’s complement where an end-around carry must be added).
• Provides an alternative way to represent negative numbers in computer arithmetic.

2. r’s Complement

The r’s complement of a number is derived by adding 1 to the $(r-1)$‘s complement of the number. This method is also applicable across different base systems and is more commonly used for arithmetic operations in digital systems due to its simplicity and efficiency.

Explanation for Different Base System

• Decimal (Base 10):
  • 10’s complement: To find the 10’s complement, first find the 9’s complement and then add 1 to the result.
  • Example:
    • Find the 10’s complement of 4567:
      • 9’s complement: 5432.
      • Add 1: 5432 + 1 = 5433.
      • Result: 5433.
• Binary (Base 2):
  • 2’s complement: To find the 2’s complement, first find the 1’s complement and then add 1 to the least significant bit (LSB).
  • Example:
    • Find the 2’s complement of 1010:
      • 1’s complement: 0101.
      • Add 1: 0101 + 1 = 0110.
      • Result: 0110.

Properties of r’s Complement

• Single Representation for Zero: Unlike the $(r-1)$‘s complement system (e.g., 1’s complement), the RR’s complement system (e.g., 2’s complement) only has one representation for zero.
• Ease of Arithmetic: Subtraction can be performed by adding the RR’s complement of the subtrahend to the minuend. If the result overflows, the carry bit is simply discarded.
• Sign Representation: The most significant bit (MSB) acts as the sign bit; 0 indicates positive, and 1 indicates negative.

Examples of Using Complements

Decimal Subtraction Using 10’s Complement:

• To subtract 1234 from 5678:
  1. Find the 10’s complement of 1234:
     • 9’s complement: 8765.
     • Add 1: 8765 + 1 = 8766.

1. 1. Add the 10’s complement of 1234 to 5678:
      markdown

      5678
      + 8766
      ——
      14444 (ignore the leftmost carry)

       

      Binary Subtraction Using 2’s Complement:

      • To subtract 101 (5 in decimal) from 1001 (9 in decimal):
        1. Find the 2’s complement of 101:
           • 1’s complement: 010.
           • Add 1: 010 + 1 = 011.

Add 011 to 1001

1001
+ 011
——
1100 (12 in decimal)

Binary Codes

When numbers, letters, or words are represented by a special group of binary symbols/combinations, we say that they are being encoded and the group of symbols is called a code. Some familiar binary codes are Decimal Codes, Error-detection Codes, The Reflected Code, Alphanumeric Codes, etc.

Decimal Codes

The representation of decimal digits by binary combinations is known as decimal codes.
Binary codes from decimal digits require a minimum of four bits. Numerous different codes
can be obtained by arranging four or more bits in ten distinct possible combinations. Some
decimal codes are:

• BCD
• Excess-3

Binary-Coded-Decimal (BCD) Code

If each digit of a decimal number is represented by its binary equivalent, the result is a
code called binary coded decimal (BCD). It is possible to assign weights to the binary bits
according to their positions. The weights in the BCD code are 8,4,2,1.

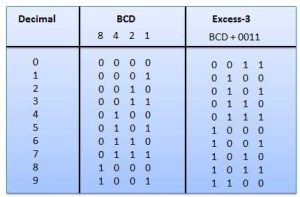
Excess-3 Code

This is an unweighted code. Its code assignment is obtained from the corresponding value
of BCD after the addition of 3.

Error-detection Codes

• An error detection code can be used to detect errors during transmission. A parity bit is
  an extra bit included with a message to make the total number of 1’s either odd or even.
• For a message of four bits parity (P) is chosen so that the sum of all 1’s is odd (in all five
  bits) or the sum of all 1’s is even. In the receiving end, all the incoming bits (in this case
  five) are applied to a “parity-check” network for checking.
• An error is detected if the check parity does not correspond to the adopted one. The parity
  method detects the presence of one, three, or any odd combination of errors. An even
  combination of errors is undetectable. Additional error-detection schemes may be needed
  to take care of an even combination of errors.

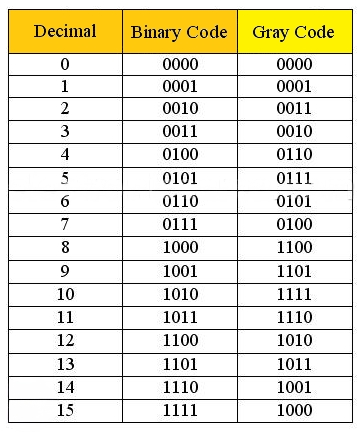
The Reflected Code/Grey Code

• The Reflected code, also called Gray code is unweighted and is not an arithmetic code;
  that is, there are no specific weights assigned to the bit positions.
• It is a binary numeral system where two successive values differ in only one bit (binary
  digit).
• For instance, in going from decimal 3 to decimal 4, the Gray code changes from 0010 to
  0110, while the binary code changes from 0011 to 0100, a change of three bits. The only
  bit change is in the third bit from the right in the Gray code; the others remain the same.

Alphanumeric Code

• To communicate, we need not only numbers but also letters and other symbols.
  In the strictest sense, alphanumeric codes are codes that represent numbers and alphabetic
  characters (letters). Most such codes, however, also represent other characters such as
  symbols and various instructions necessary for conveying information.
• The ASCII is the most common alphanumeric code.

ASCII Code

ASCII is the abbreviation for the American Standard Code for Information Interchange. ASCII is a universally accepted alphanumeric code used in most computers and other electronic equipment. Most computer keyboards are standardized with the ASCII. When we enter a letter, a number, or a control command, the corresponding ASCII code goes into the computer.

• ASCII has 128 characters and symbols represented by a 7-bit binary code. Actually, ASCII can be considered an 8-bit code with the MSB always 0. This 8-bit code is 00 through 7F in hexadecimal.
• The first thirty-two ASCII characters are non-graphic commands that are never printed or displayed and are used only for control purposes. Examples of the control characters are “null,” “line feed,” “start of the text,” and “escape.”
• The other characters are graphic symbols that can be printed or displayed and include the
  letters of the alphabet (lowercase and uppercase), the ten decimal digits, punctuation signs
  and other commonly used symbols.

 Extended ASCII characters

In addition to the 128 standard ASCII characters, there are an additional 128 characters that
were adopted by IBM for use in their PCs (personal computers). Because of the popularity of
the PC, these particular extended ASCII characters are also used in applications other than
PCs have become essentially an unofficial standard. The extended ASCII characters are
represented by an 8-bit code series from hexadecimal 80 to hexadecimal FF.