Chemical Kinetics: Reaction Rates, Equations and Mechanisms

Chemical Kinetics

Chemical kinetics is the branch of chemistry that deals with studying the rates of chemical reactions, the factors affecting these rates, and the mechanisms by which the reactions occur. It involves understanding how different conditions, such as concentration, temperature, and the presence of catalysts, influence the speed at which reactions proceed. This field helps elucidate the step-by-step sequence of elementary reactions that lead to the overall transformation of reactants into products.

Concept of chemical reaction

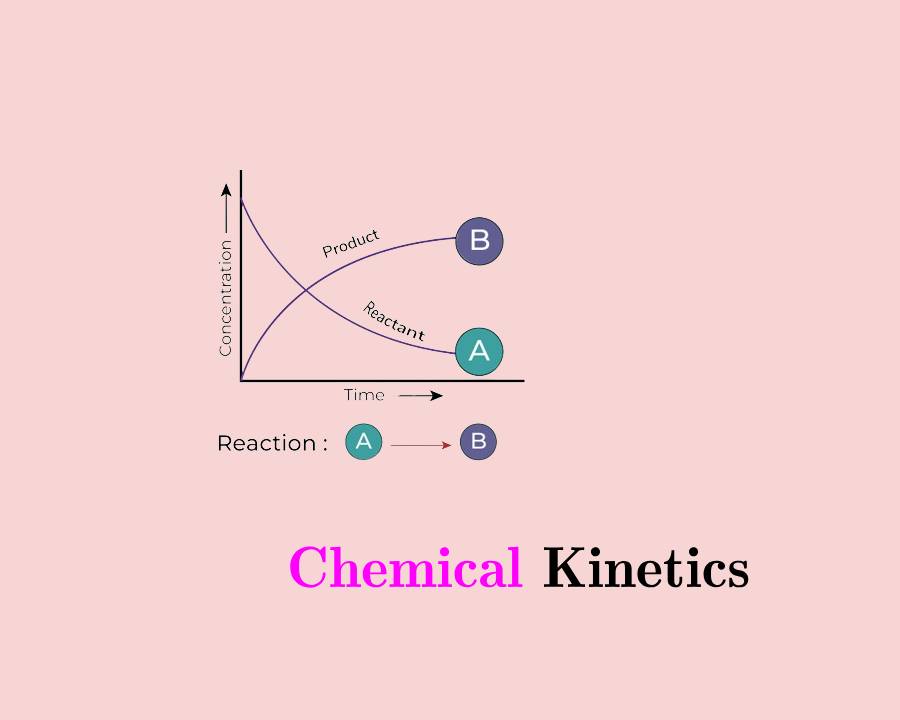
The rate of reaction is defined as a decrease in the concentration of reactant or an increase in product per unit of time. It is also defined as the increase in concentration of the product per second.

E.g: A à B (general reaction)

So, Rate = −Δ[A]Δt−Δ[A]Δt

 

Average rate of reaction

It is the ratio of reaction measured for a long interval of time. Let us consider a general reaction.

A à B

Let, the initial concentration of reactant at time t₁ , be [A₁] and final concentration be [A₂]

So, Average rate (R) = (change in concentration)/(Change in time)(change in concentration)/(Change in time)

Or, –A2−A1t2−t1A2−A1t2−t1

= −ΔAΔt−ΔAΔt

Here, [A₁] is greater than [A₂]. So, ΔΔA = (A₂ – A₁). Now, the change in concentration of the product is positive.

i.e. C₂ – C₁ = +ve.

So, Rate(R) = ΔCΔtΔCΔt

Where, ΔCΔC = C₂ – C₁

And ΔΔt = t₂ – t₁.

 Instantaneous Rate of reaction:

The average rate obtained by finding the slope of the curve is not always useful. They cause a large interval of time during which the rate of reaction changes significantly. If the interval is small the rate is referred to as the instantaneous rate and is written as:

Rate = −d[r]dr−d[r]dr

 

Factors affecting the rate of reaction

(i) Concentration:

The rate depends on the concentration of the reaction. Initially, a reaction occurs due to high concentration of reactant. With the passing of time concentration of reactant goes on decreasing which results decrease in rate. It is given in the fig:

 

 

Factor affecting rate of reaction by concentration:

(ii) Temperature:

According to kinetic molecular theory, average kinetic energy is directly proportional to absolute temperature. The rate of reaction increases with an increase in temperature. This is because the average kinetic energy of the reactant molecule increases as the temperature is increased. For every 10°C rise the temperature rate is increased by 2 – 3 folds. The effect of temperature on rate can be explained based on Maxwell’s distribution of molecular velocity.

 

The fraction of molecules having very high velocity increases with an increase in temperature as shown in Fig. This result increases K.E. Thus, the rate increases fraction with the molecule increase in temperature.

 

(iii) Catalyst:

It is a substance which accelerates or retards the rate of reaction. In general, the catalyst increases the rate of reaction. It increases the rate by providing a new path and lowering the activation energy. The effect of the catalyst is shown in Fig.

 

 

 

Factor affecting rate of reaction by catalyst:

 

 

(iv)Surface area: The larger the surface area of the reaction the faster the rate of reaction. It has been observed that if one of the reactants is in a solid, then the rate of the reaction depends upon the state of subdivision of the solid. This fact is supported by the general observation that freely divided solids react faster than massive substance

 

Rate law, Rate constant, and its units

Rate law:  The rate law of a given reaction depends on the concentration of reactants at a fixed temperature is known as rate law.

Let us consider a general reaction

aA + bB + cC à Products.

So, Rate ∝∝ [A]^P[B]^a[C]^r

Rate = k[A]^P[B]^a[C]^r ….(i)

 

Rate constant: The rate of the reaction when the concentration of each of the reacting species is unity at a given temperature is known as Rate constant

[A]=  [B]= 1 MOL L^-1 then,

R=    K [1] [1]   or rate,=  [  R=K]

 

Types of the order of reaction

 

First order of reaction: A chemical reaction in which the rate of reaction depends upon one concentration is known as a first-order reaction.

Units of first-order reaction = min^-1 or sec^-1.

 

Second-order reaction: A chemical reaction in which the rate depends upon the second power of the initial concentration of reactant is called a second-order reaction.

Unit of second order reaction mol^-1 L sec^-1.

 

 Third-order reaction: A Chemical reaction in which the rate depends upon the third power of the initial concentration of the reactant is called a first-order reaction. Unit of third order reaction = mol^-2 L² sec^-1.

Zero-order reaction: A chemical reaction in which the rate of reaction is independent of the concentration of the reactant is called a third-order reaction.

Unit of zero order reaction:  mol^-1  L^-1 S^-1

 

Order and molecularity of the reaction

 

The differences between the order and molecularity of the reaction are given below:

Order of reaction	Molecularity of reaction
It is the total number of concentration variables that affect the rate of reaction.	It is the total no. of chemical species involved in the reaction.
It is an experimentally determined value.	It is a theoretical concept. i.e. assigned parameters.
It changes with changes in temperature and pressure.	It doesn’t change with changes in temperature and pressure.

 

Integrated law for a first-order reaction

Let us consider general first-order reactions,

A à Product.

Let the initial concentration of A is ‘a’ moles and x moles L^-1 of it get changed to products after ‘t’. Thus, the concentration of reactant A left after time ‘t’ is (a – x) moles per liter i.e.

A à product

A = ‘a’ moles L^-1

(a – x) moles L^-1

 

Products: Initially (At time ‘t’)

According to the law of mass action the rate of a first reaction of any time ‘t’ is directly proportional to the concentration of reactant present in the system of that instant. Therefore, it is given by:

Rate = −d[A]dt=−d(a−x)dt=k1(a−x)−d[A]dt=−d(a−x)dt=k1(a−x)

Or, dxdt=k1(a−x)dxdt=k1(a−x)….(i)

Rearranging equation (i), we get,

Or, dxa−x=k1dtdxa−x=k1dt

On integrating the above equation, we get,

Or, ∫dxa−x=∫k1dt∫dxa−x=∫k1⁡dt

= -ln(a – x) = k₁t + I …(ii)

Where, I is integration constant, When t = 0, x = 0,

Thus, -ln(a – 0) = k₁ * 0 + I

So, I = -lna.

Substituting, the value of I in equation (ii), we have,

Or, – ln(a – x) = k₁t – lna

Or, k₁ = 1t1t.lnaa−xaa−x

Or, K₁ = 2.303t.logaa−x2.303t.log⁡aa−x ….(iii)

So, Equation (iii) is known as the integrated rate law for a first-order reaction.

The value of the rate constant of a first-order reaction is independent of the units of concentration used. This can be proved as follows:

Let the unit of concentration be changed. So, in the new unit system, the value of concentration becomes ‘m’ times of its original value, then from the equation (iii), we can write,

Or, K₁ = 2.303t.logmama−mn2.303t.log⁡mama−mn

Or, K = 2.303t.logaa−x2.303t.log⁡aa−x

This is the same as equation (iii).

 

Half-life reaction of first order

The time required to decompose exactly half of the initial concentration of reactant is known as the half-life period. It is denoted by t_1/2.

For 1^st order reaction, we can write;

K­₁ = 2.303t2.303t.log aa−xaa−x, where the initial concentration of reactant and (a – x) concentration after time ‘t’ seconds.

For t_1/2 life period,

t = t_1/2 and (a – x) = a2a2.

So, K₁ = 2.303t122.303t12.log(aa2)(aa2)

Or, t_1/2 = 2.303K1.log22.303K1.log2

Or, t_1/2 = 0.693K10.693K1

i.e. t_1/2∝∝1k11k1.

Thus, t_1/2of the first-order reaction is independent of the initial concentration of the reactant.

 

Or,

In a first-order reaction,

A = product.

t = 0 [A] = a product = 0

t, [A] = (a – x) , product = x.

Then, Rate = −d[A]dt=dxdt=k[A]−d[A]dt=dxdt=k[A]

Or, dxdt=k(a−x).dxdt=k(a−x).

Or, dxa−x=dt.Kdxa−x=dt.K

Integrating on both sides,

Or, ln(a – x) = kt + c

At t = 0, x = 0

Then –lna = c

Putting the value of C,

– ln(a – x) = kt – lna

Or, kt = ln aa−xaa−x

Or, t = 1k.ln.aa−x1k.ln.aa−x

At, t_1/2, X = a2a2.

Then, t_1/2 = 1kln.aa−a21kln.aa−a2

Or, t12=1kln2t12=1kln2

Or, t12=0.693Kt12=0.693K

[So, t12=0.693kt12=0.693k]

Thus, half – the life of the first order is independent of the initial concentration

 

Collision theory of reaction rate:

According to this theory, all molecule collisions are not effective only a fraction of molecules colliding with sufficient kinetic energy leads to the formation of a product called an effective collision.

Thus, molecule collision occurring with sufficient kinetic energy which leads to the formation of a product is called effective collision. The molecule collision occurring with insufficient K.E. and improper orientation is called an inefficient collision.

Consider the formation of hydrogen iodide by the reaction between H₂ and I₂.

H₂ + I₂ = 2HI

This can be diagrammatically represented as:

Every substance has a definite amount of energy due to “to and fro” motion is called average energy [E_av]. In order to cause a chemical change, reacting species should cross over the energy barrier as shown in the energy profile diagram. The minimum amount of energy required to cross the energy barrier is called activation energy [E_a]. The minimum amount of energy associated with an activated complex that can cause a chemical change is called threshold energy (E_th). Therefore, threshold energy is the sum of average (E_a) and activation energy (E_av).

So, E_th = E_av + E_a

So, E_a = E_th – E_av

Thus, activation energy is the additional amount of energy supplied to reactants to cause a chemical change.

This theory is called collision theory for bio – molecular reaction

Collision theory of reaction rate

 

The concept of activation energy as the energy barrier activates complex and affects of catalyst on the rate of reaction

Every substance has a definite amount of energy due to “to and fro” motion is called average energy [E_av]. In order to cause a chemical change, reacting species should cross over the energy barrier as shown in the energy profile diagram. The minimum amount of energy required to cross the energy barrier is called activation energy [E_a]. The minimum amount of energy associated with an activated complex that can cause a chemical change is called threshold energy (E_th). Therefore, threshold energy is the sum of average (E_a) and activation energy (E_av).

So, E_th = E_av + E_a

So, E_a = E_th – E_av

Thus, activation energy is the additional amount of energy supplied to reactants to cause a chemical change.

This theory is called collision theory for biomolecular reaction

Effect of catalyst on the rate of reaction

It is a substance which accelerates or retards the rate of reaction. In general, the catalyst increases the rate of reaction. It increases the rate by providing a new path and lowering the activation energy. The effect of catalysis in shown in Fig.

 

 

Catalysts affect the rate of a reaction by providing an alternative reaction pathway with a lower activation energy. This increases the rate of reaction in the following ways:

 

1. Lower Activation Energy: Catalysts lower the energy barrier for the reaction, making it easier for reactant molecules to convert into products. This results in an increased reaction rate at the same temperature.

 

2. Formation of Intermediate Complexes: Catalysts can form intermediate complexes with reactants. These intermediates decompose to yield the final products, facilitating the reaction process.

 

3. Increase in Collision Frequency: Catalysts can orient reactant molecules in a favorable manner, increasing the frequency and effectiveness of collisions between reactant molecules.

 

4. Surface Area of Solid Catalysts: For heterogeneous catalysts, the surface area is crucial. A larger surface area provides more active sites for the reaction, thus increasing the reaction rate.

 

5. Concentration of Catalyst: Increasing the concentration of the catalyst generally increases the reaction rate, as more catalytic sites are available for the reactant molecules.

 

6. Physical State of the Catalyst: The physical state (solid, liquid, or gas) and the dispersion of the catalyst can affect its efficiency. Finely divided catalysts have larger surface areas and are more effective.

 

7. Presence of Inhibitors or Promoters: Certain substances can affect the activity of a catalyst. Inhibitors decrease the effectiveness of catalysts, while promoters enhance their activity.

 

8. Temperature: Although catalysts provide an alternative pathway with a lower activation energy, temperature still plays a role. Higher temperatures generally increase the rate at which the catalyst and reactants interact.

 

These factors collectively determine the efficiency and effectiveness of a catalyst in increasing the rate of a chemical reaction.